Power Formula with Power Factor | A Simple Explanation

Understanding the power formula with power factor is crucial when calculating electrical power in AC (alternating current) circuits. In AC systems, the current and voltage can fall out of sync, which impacts the actual power that can be utilized. This is where the power factor becomes important. The power factor (PF) measures how effectively the power is being used by accounting for the phase difference between current and voltage.

How to find apparent and reactive power of motor | Energy Manager exam question

Introduction to AC Circuits

Before diving into the power formula with power factor, it’s essential to understand what an AC circuit is and why it’s important in electrical systems.

Alternating Current (AC) is a kind of electricity where the flow of energy keeps switching directions back and forth. This is different from Direct Current (DC), where the electricity flows in just one direction without changing. In AC, the direction flips many times every second.

This oscillation is typically measured in Hertz (Hz), with standard frequencies being 50 Hz in many parts of the world and 60 Hz in others, such as in North America.

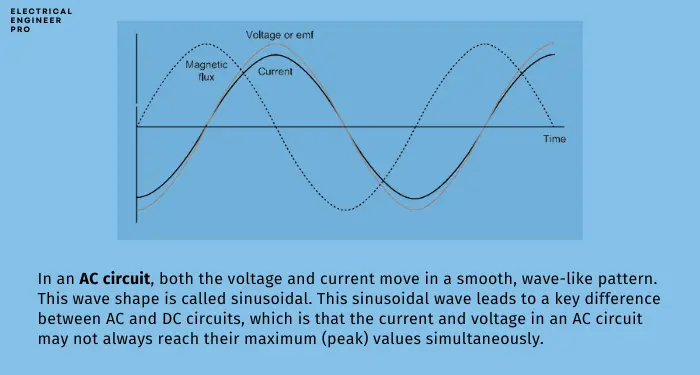
In an AC circuit, both the voltage and current move in a smooth, wave-like pattern. This wave shape is called sinusoidal. This sinusoidal wave leads to a key difference between AC and DC circuits, which is that the current and voltage in an AC circuit may not always reach their maximum (peak) values simultaneously. 

This phase difference between current and voltage is where concepts like power factor come into play, as it directly affects how efficiently power is used in the circuit.

Understanding the basic behavior of AC circuits—where voltage and current fluctuate and can be out of sync—is crucial for grasping how electrical power is calculated and optimized using the power formula with power factor.

Energy Manager | Calculate Power Factor & Payback Period

What is Power Factor

Let’s talk about power factor which is a key player when it comes to understanding the power formula with power factor in AC circuits.

Simply put, the power factor tells us how well the electrical power is being used to do actual work, like running your appliances or lighting up a room.

As explained, in AC circuits, voltage and current don’t always sync perfectly. This is mainly due to devices like motors or capacitors, which cause the current to either lag behind or race ahead of the voltage. This phase difference is what the power formula with power factor helps us understand.

The textbook definition says, Power Factor is the cosine of the angle between the voltage and current.

But what does that mean? 

Well, it’s a way of saying how much of the power is actually doing something useful versus how much is just bouncing back and forth without doing any real work.

Power factor is an important component because if it’s low, your AC electrical system will not run smoothly as it should.

You’ll need more current to get the same amount of work done, which decreases the efficiency and costs you more on your electricity bill. Plus, utilities might even charge penalties if your power factor is too low.

Fortunately, there are ways to improve power factor, like adding capacitors to the circuit. This not only helps your system run more efficiently but also makes the power formula with power factor a much more accurate tool for figuring out how much power you can really use.

To sum it up, power factor is all about making sure the power you’re paying for is being used effectively. And when you understand it through the power formula with power factor, you’re one step closer to running a more efficient and cost-effective electrical system.

How Air Circuit Breakers (ACB) Work | Explained

Why Power Formula with Power Factor Matters

To grasp the significance of the power formula with power factor, it’s essential to look at how these elements interact in an AC circuit.

Unlike direct current (DC) circuits, AC systems often include components like inductors and capacitors that can cause a phase shift between voltage and current. This phase shift is what makes the power factor so critical.

Breaking Down the Power Formula

The basic power equation, P = I × V, is straightforward which tells us that power (P) equals current (I) multiplied by voltage (V). However, in AC circuits, especially those with reactive components, the power factor must be considered to accurately calculate usable power.

Instantaneous Power

At any given moment, power is the product of the current and voltage at that specific time, expressed as P(t) = I(t) × V(t). This instantaneous power fluctuates constantly in AC systems, so while it’s useful for real-time analysis, it doesn’t provide a complete picture of energy usage.

Here, t represents time, indicating that the values of I(t) and V(t) vary with time, and the product of these values gives the power at that specific instant.

Average Power

For practical applications, we focus on average power over a full AC cycle, where the power formula with power factor becomes essential. This formula helps determine the real power that can be harnessed over time, rather than just at a single instant.

Essential Guide to Voltage Unbalance

Power Formula with Power Factor in Different Loads

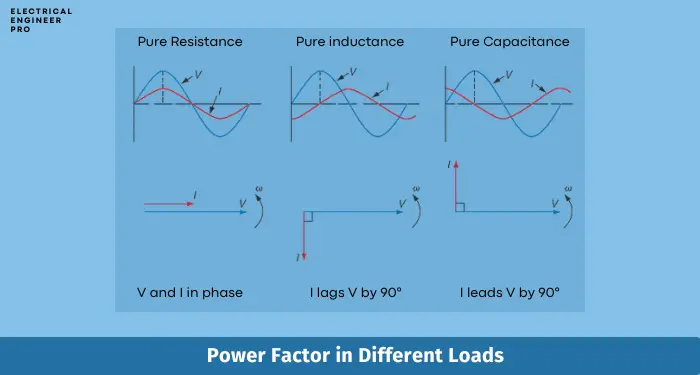
Resistive Loads

In circuits with purely resistive elements (like heaters or incandescent bulbs), the current and voltage are perfectly in sync, meaning they rise and fall together.

Here, the power formula with power factor simplifies to P_ave = I_rms × V_rms, as the power factor is 1. This means all the power is effectively converted into work, such as producing heat or light.

Reactive Loads

When inductors or capacitors are involved, the situation changes. These components create a phase difference between the current and voltage.

For instance, with inductive loads like motors, the current falls behind the voltage, while with capacitive loads, the current moves ahead of the voltage.

This phase difference causes some power to be temporarily stored and later returned to the system, resulting in what’s called negative instantaneous power. Here, the power formula with power factor becomes essential for calculating the actual power available for doing work.

Importance of Power Factor in the Power Formula

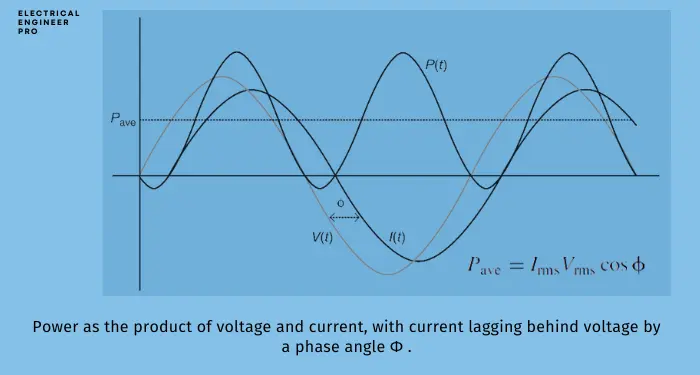
The reduction in average power due to the phase shift between voltage and current is quantified by the power factor. The power factor is defined as the cosine of the phase angle ϕ between the voltage and current wave-forms:

The full power formula with power factor is:

P_ave = I_rms × V_rms × cos(ϕ)

Here, cos(ϕ) is the power factor (pf). The power factor ranges from 0 to 1:

• A power factor of 1 (or 100%) indicates that the voltage and current are perfectly in phase, meaning all the electrical power is being used for productive work. This scenario is typical of purely resistive loads like incandescent light bulbs or electric heaters.

• A power factor less than 1 indicates that some of the power is not being used effectively. Instead, it is circulating back and forth between the source and the reactive components (inductors or capacitors) without doing any real work. This leads to inefficiencies in the system.

Types of Power in AC Circuits

In AC circuits, current and voltage do not always reach their peak values simultaneously, leading to the introduction of three distinct types of power: active power, reactive power, and apparent power. Understanding these types is crucial when applying the power formula with power factor.

Active Power (P)

Active power, also known as real power, is the power that performs useful work in the circuit. It’s the power that drives motors, produces light, and generates heat.

Measured in watts (W), active power represents the portion of power that is perfectly in phase with both the voltage and current wave-forms. This power is what we’re typically billed for, as it directly correlates to the energy consumed by devices.

Reactive Power (Q)

Unlike Active power, Reactive power is the energy that constantly flows back and forth between the power source and the devices in a circuit because of inductive or capacitive elements.

However, it’s crucial for keeping voltage levels stable, which is necessary for the proper function of equipment like motors and transformers.

Measured in volt-amperes reactive (VAR), reactive power is vital in AC systems, as it helps manage the energy stored and released in components like inductors and capacitors.

Apparent Power (S)

Apparent power is the total power supplied in an AC circuit, combining both active power, which does useful work, and reactive power, which supports the system. It’s measured in volt-amperes (VA) and gives a complete picture of the power needs in the circuit.

Understanding apparent power is important for sizing equipment, determining system capacity, and evaluating overall efficiency.

Relationship Between Active, Reactive, and Apparent Power

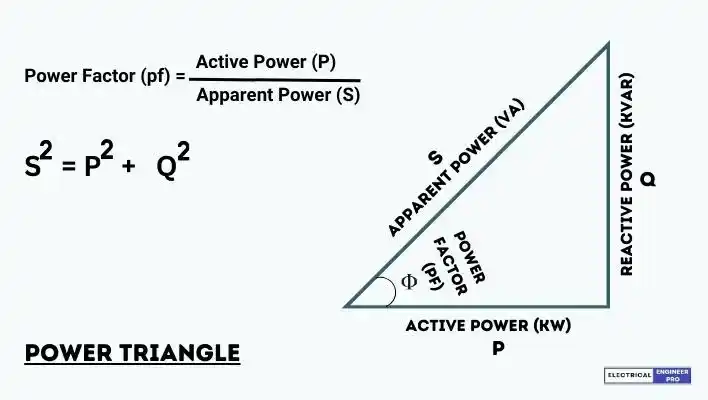
The relationship between active power (P), reactive power (Q), and apparent power (S) can be visualized using the power triangle. This right-angled triangle graphically shows how these three types of power are interconnected:

• P (Active Power): Represented by the horizontal side, indicating the power that does useful work.
• Q (Reactive Power): Represented by the vertical side, showing the power that oscillates between the source and the load.
• S (Apparent Power): The hypotenuse of the triangle, representing the total power in the circuit.

Power Triangle and Its Importance

The power triangle is a useful tool for visualizing the relationships between active power, reactive power, and apparent power. By understanding this triangle, engineers and technicians can better manage power systems, improve efficiency, and ensure reliable operation. Proper management of the power triangle, particularly by optimizing the power factor, is essential for minimizing energy losses and maintaining system stability.

Useful formulas

• Active power P (in kW)
  • Single phase (1 phase and neutral): P = V x I x Cos Φ
  • Three phase (3 wires + neutral): P = √3 x U x I x Cos Φ

• Reactive power Q (in kvar)
  • Single phase (1 phase and neutral): Q = V x I x Sin Φ
  • Three phase (3 wires + neutral): Q = √3 x U x I x Sin Φ

• Apparent power S (in kVA)
  • Single phase (1 phase and neutral): S = V x I
  • Three phase (3 wires + neutral): S = √3 x U x I

V = Voltage between phase and neutral
U = Voltage between phases
I = Line current
Φ = Phase angle between vectors V and I. 

Why √3 is used in 3-Phase Power with Power Factor Formula

The formula for three-phase power depends on whether the system is balanced and the type of connection (star or delta). For a balanced three-phase system, the total power can be calculated using the following formula:

Total Power (P) = √3 × V_L × I_L × cos(ϕ)

Where:

• P is the total power in watts (W).
• √3 is the constant (approximately 1.732).
• V_L is the line voltage (the voltage between any two phases).
• I_L is the line current (the current flowing in each phase).
• cos(ϕ) is the power factor (the cosine of the phase angle between the voltage and current).

Why the Constant √3 is Used ?

The mysterious √3 (approximately 1.732). This constant comes into play because, in a three-phase system, the voltage between any two lines is higher than the voltage from a line to the neutral point (in a star connection). This difference naturally creates a factor of √3 when you’re converting between these voltages.

Star (Y) Connection

In a star connection, the line voltage (VL) is √3 times the phase voltage (VPh). Mathematically,

VL​=√3 x Vph (Equation no. 1)

Similarly, the line current (IL) is equal to the phase current (IPh).

IL​=IPh​

Power Calculation

Total Power in each phase is,

Pphase = Vph × Iph × cos(ϕ)

Total power in a three-phase system is the sum of the power in all three phases:

P = 3 x Pphase = 3 x Vph × Iph × cos(ϕ)

Substituting equation no. 1 in Vph and simplifying we get,

Power (P) = √3 × VL × IL × cos(ϕ)

The constant √3 is used in the formula to account for the difference between the line voltage and phase voltage in a three-phase system, ensuring the correct calculation of total power.

Conclusion

Understanding the power formula with power factor is key to accurately calculating and optimizing power usage in AC circuits. While the basic equation P = I × V is fundamental, incorporating the power factor is crucial in systems where current and voltage are out of phase. By considering the different types of power—active, reactive, and apparent—and how they relate through the power triangle, you can better analyze and design efficient electrical systems.

FAQs