This article will guide you through the process of determining the current power factor of a plant and calculating the simple payback period after enhancing the power factor.
To illustrate these concepts, we will use the problem statement given in the 12th Energy Manager exam, centered around power factor improvement.
Throughout the explanation, you’ll gain insights into key parameters like Power Factor, Contract Demand, Maximum Demand and Simple Payback Period.
These parameters hold significance for energy managers in industrial plants, forming the foundation for effective energy management practices.
Also Read: How to find apparent and reactive power of motor | Energy Manager exam question
Problem Statement
During the energy audit of a process plant, the electricity bills were analyzed. The plant has a contract demand of 5000 kVA with the power supply company. The average maximum demand of the plant is 3850 kVA/month at a power factor of 0.95. The maximum demand is billed at the rate of Rs.600/kVA/month. The minimum billable maximum demand is 75 % of the contract demand. An incentive of 0.5 % reduction in energy charges component of electricity bill are provided for every 0.01 increase in power factor over and above 0.95. The average energy charge component of the electricity bill per month for the plant is Rs.18 lakhs.
The plant decides to improve the power factor to unity. Determine the power factor capacitor kVAr required, annual reduction in maximum demand charges and energy charge component. What will be the simple payback period if the cost of power factor capacitors is Rs.1100/kVAr.
Definitions
Energy managers utilize parameters such as Power Factor, Contract Demand, Maximum Demand and Simple Payback Period as essential tools in energy management.
By closely monitoring and understanding these parameters, energy managers can implement effective strategies to enhance energy efficiency, reduce costs, ensure compliance with contractual obligations, and optimize overall energy consumption in industrial plants.
Before going into the solution for the given problem statement, let’s familiarize ourselves with the concepts of Power Factor, Contract Demand, Maximum Demand and Simple Payback Period.
Power Factor
The total power requirement can be broken down into two components, as depicted in the power triangle
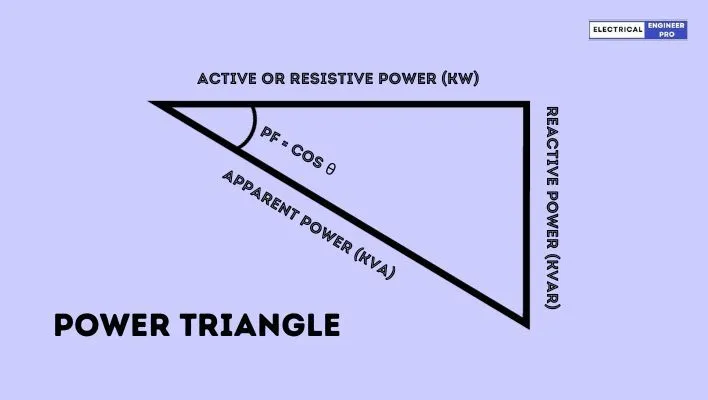
In the diagram you can see there are two sides: the resistive portion or Kilowatt (KW) and the reactive portion, Kilovolt Ampere Reactive (kVar).
The resistive portion measured in KW, is in-phase with the power source and represents the active power, which is directly converted into useful work.
On the other hand, the reactive portion, measured in kVar, is 90 degrees out of phase with the resistive portion. Its role is to establish the magnetic field flux required for inductive devices, but it is generally non-usable power.
For example, imagine an electric motor in an industrial setting. The resistive portion (KW) represents the actual power consumed by the motor, contributing to the mechanical work done by the motor.
Meanwhile, the reactive portion (kVar) is necessary for creating magnetic fields in the motor but does not directly contribute to the useful work output.
The hypotenuse of the power triangle represents the overall Kilovolt-Ampere (kVA) or apparent power. The angle formed between the resistive portion (KW) and the apparent power (kVA) is known as the power factor angle.
Understanding and optimizing the power factor angle is crucial for efficient energy utilization, as it indicates the proportion of power that is effectively converted into useful work.
Also Read: Step-by-Step Guide to solve Energy Managers Exam Question on Motor Energy Savings
Contract Demand
Contract Demand refers to the maximum amount of electrical power that an industrial or commercial facility or consumer has agreed upon in a contract with the electricity supplier.
It represents the upper limit of power that the consumer is committed to using during a specified period, typically measured in kilowatts (kW) or megawatts (MW), kVA (Kilo Volt Ampere) or MVA (Mega volt Ampere).
The contract demand is a key aspect of electricity supply agreements and is established based on the consumer’s anticipated power requirements.
Here’s an example to illustrate Contract Demand:
Let’s consider a manufacturing facility that requires a consistent and reliable supply of electricity for its operations. The facility enters into a contractual agreement with the electricity supplier to establish a Contract Demand of 500 kilowatts (kW). This means that, according to the terms of the contract, the facility commits to keeping its power consumption within the limit of 500 kW.
If, during normal operations, the facility consistently operates below the contracted 500 kW, it will be billed based on this agreed-upon demand. However, if the facility exceeds the 500 kW limit, it may incur additional charges or penalties specified in the contract.
In summary, Contract Demand is a crucial aspect of electricity supply agreements, allowing consumers to plan and manage their power needs efficiently while providing electricity suppliers with a basis for determining pricing and ensuring a reliable power supply.
Maximum Demand
Maximum Demand, often denoted as “MD,” is the highest level of electrical power consumption within a specified period, typically measured in kilowatts (kW) or megawatts (MW).
It represents the peak power requirement during a specific time-frame, which is crucial for both consumers and electricity providers to understand and plan for efficient energy distribution.
Let us take an example to clarify Maximum Demand:
Consider a commercial building that operates various electrical equipment such as lighting, air conditioning, machinery, and computers. Throughout a particular month, the building’s power consumption fluctuates based on the intensity of its activities. The highest level of power usage recorded during this period is the Maximum Demand.
Let’s say the building experiences its highest power consumption of 200 kW on a particularly hot day when the air conditioning systems, machinery, and lighting are all in heavy use simultaneously. In this scenario, 200 kW represents the Maximum Demand for that specific moment.
Maximum Demand is crucial for electricity providers in capacity planning. Knowing the peak power requirement helps them allocate resources, plan for infrastructure upgrades, and ensure that the electrical grid can handle the highest levels of demand without issues such as overloading or disruptions.
For Energy Managers, understanding their Maximum Demand is essential for optimizing their energy usage, avoiding peak demand charges, and implementing strategies to manage energy consumption during periods of high demand. It is a key parameter used in designing and sizing electrical systems to meet the maximum power needs of a facility.
Simple Payback Period
The payback period signifies the duration, measured in years, required to recoup the initial investment (capital cost) based solely on annual net savings. It serves as a metric to determine when the investment will recover itself, influencing the necessary financing terms.
As the payback period nears its completion, all project capital costs are recuperated, and any subsequent cost savings are deemed clear profit. A shorter payback period is indicative of a more appealing project.
The Simple Payback Period is calculated using the formula:
[latex]Simple Payback Period = \frac{Capital Costs}{Annual Net Savings}[/latex]
The term “simple” is used to emphasize that the calculation does not consider the time value of money. Annual net savings represent the achieved cost savings after covering all operational costs.
Example: Suppose a company invests $100,000 in energy-efficient equipment. The annual net savings resulting from this investment, after accounting for operational costs, amount to $20,000. Using the Simple Payback Period formula:
[latex]Simple Payback Period = \frac{100,000}{20,000}[/latex] = 5 years
This means the company would recover its initial $100,000 investment in the energy-efficient equipment within 5 years, considering only annual net savings. Any savings beyond this period would be considered clear profit.
Also Read: Calculate motor temperature rise from unbalanced voltage | Energy Manager Exam question
Difference Between Contract Demand and Maximum Demand
| Contract Demand | Maximum Demand |
| It is the maximum amount of electrical power that a consumer has agreed upon in a contract with the electricity supplier. It represents the upper limit of power that the consumer commits to using. | It is the highest level of electrical power consumption recorded within a specific period. It represents the peak power requirement of a consumer during a given time-frame. |
| It is a contractual obligation and is typically specified in the agreement between the consumer and the electricity supplier. It is a pre-determined value agreed upon in advance. | It is a measurement taken over a specific period, often determined based on the highest power usage during a day, a month, or another defined time frame. |
| The consumer is usually billed based on the agreed-upon Contract Demand. Exceeding this limit may result in additional charges or penalties, as specified in the contract. | While it doesn’t directly impact billing, understanding Maximum Demand is crucial for infrastructure planning, as exceeding the capacity associated with Maximum Demand may lead to inefficiencies or require upgrades. |
| It is a fixed value agreed upon in the contract and remains constant unless the contract is renegotiated. It is not subject to frequent changes. | It is a dynamic value that can vary based on the actual power consumption patterns. It is measured periodically to capture the highest level of demand during specific time intervals |
| Consumers have more control over their Contract Demand, and it provides a level of predictability in terms of the maximum power they commit to using. | It is less predictable and may vary based on unforeseen circumstances or changes in operational patterns, providing insights into the highest load the system may need to accommodate. |
Also Read: How to find 3-phase AC motor parameters? Energy Manager exam question.
Solution To Problem Statement
Given:
| Contract Demand | 5000 kVA |
| Maximum Demand | 3850 kVA/month @ 0.95 power factor |
| Maximum Demand Billing Rate | Rs.600/kVA/month |
| Power factor θ1 | 0.95 |
| Improved Power factor θ2 | 1 |
| Capacitor Cost | Rs.1100/kVAr |
Calculate:
| Capacitor kVAr required | ? |
| Annual reduction in maximum demand charges | ? |
| Energy charge component | ? |
| Simple payback period | ? |
Solution:
Firstly we need to calculate capacitor kVar required but to do that we have to know the KW drawn by the plant.
| As MD is 3850 kVA at 0.95 pf, so KW drawn | = kVA X p.f. |
| = 3850 X 0.95 | |
| 3657.5 KW |
Now the kVar required,
| kVar required to improve power factor from 0.95 to 1 | = kW ( tan θ1 – tan θ2) |
| = kW [tan (cos-1θ1) – tan (cos-1θ2)] | |
| = 3657.5 [tan (cos-10.95) – tan (cos-11)] | |
| = 3657.5 [tan (18.19) – tan (0)] | |
| = 3657.5 [0.328 – 0] | |
| Capacitor Required | = 1199.66 = 1200 kVar |
Further the cost of capacitors
| Total Cost of capacitors @Rs.1100/kVAr | = 1200 kVAr X Rs 1100 |
| = Rs.13,20,000 |
Reduction in Demand charges
| Maximum demand at unity power factor (kVA) | [latex] = \frac{KW}{p.f.}[/latex] |
| [latex] = \frac{3657.5}{1}[/latex] | |
| [latex] = {3657.5}[/latex] KW | |
| It given that maximum demand is 75 % of the contract demand | = 5000 X 0.75 |
| =3750 kVA | |
| ∴ Reduction in Demand charges | = 3850 – 3750 |
| = 100 kVA | |
| Now the plant has to pay MD charges on minimum billable demand of 3750, and not on the improved MD of 3657.5 kVA in this case | |
| So the Annual Reduction in Demand Charges | = 100kVA/month x 12 months x Rs.600 kVA/ month |
| = Rs.7,20,000 |
Annual Reduction in Cost
| Percentage reduction in energy charge from 0.95 to 1 @ 0.5 % for every 0.01 increase | 2.5% |
| Monthly energy cost component of the bill | Rs.18,00,000 |
| Reduction in energy cost component | [latex] = 1800000 \times \frac{2.5}{100}[/latex] |
| = Rs.45,000/month | |
| Rs.45,000 x 12 | |
| Annual reduction in energy cost component | = Rs.5,40,000 |
Finally, The Payback Period comes to,
| Annual Net Savings in electricity bill | = Rs.7,20,000 + 5,40,000 |
| = Rs.12,60,000 | |
| Investment (Capital Cost) | Rs.13,20,000 |
| Payback period | [latex] = \frac{13,20,000}{12,60,000}[/latex] |
| = 1.04 years or 12.4 months |
Answer
| Capacitor kVAr required | 1199.66 = 1200 kVar |
| Annual reduction in maximum demand charges | Rs.7,20,000 |
| Energy charge component | Rs.5,40,000 |
| Simple payback period | 1.04 years or 12.4 months |
Also Read: Energy Manager Exam | Co-generation power plant Numerical problem with solution






